某鍛冶検定　解答と解説　#dq10

（問題）
温度1000℃、緑ゾーンまであと20～26のところでねらい打ちをしたら24進みました。このゲージが理想値で止まっている(本会心が出ていた)確率を求めなさい。
注：理想値があと２０～２６のどこになるか確率はそれぞれ同じ(1/7ずつ)とします。というかそうでないと複雑になりすぎますｗ
（解答と解説）
全てのパターンを取り出して表にする。

24が出る確率Ｐ（Ａ）＝9/49
24が出てかつそれが理想値になっている確率Ｐ（Ａ∩Ｂ）＝7/49
ベイズの定理により、求める確率Ｐ（Ａ｜Ｂ）
＝Ｐ（Ａ∩Ｂ）／Ｐ（Ａ）
＝(7/49）／(9/49）
＝7/9（解答）
( ﾟдﾟ)
わかりやすく書きます。
表を見てください。

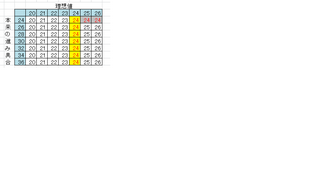
この中で、24が出るパターンが９つあるのがわかると思います。（そもそもで言えば、会心が出たとき24になる確率が9/49）
理想値が24であるケースは、当然理想値＝24の列になりますから７パターンあります。
「24進んだ」という条件の中で、理想値をはずしているパターンは２つあります。
つまり、９つあるうちの７つが理想値になっているので正解は7/9です。
…これで直観的にわかるでしょうか。
もしこれを「会心が出た（けれど24かどうかは気にしない）」という状態で考えると、理想値で止まっている確率は47/49あります。
表のうち、右上２つを除いた全てのパターンで理想値になっていますね。
どう違うの？と思われた方は、もう一度ゆっくり考えてみてください。
細かな技術になりますが、このことは特に戻りゲージタイプの鍛冶で使えるケースが多いです。意図せず（あるいは意図して）会心が出て、緑ゲージの手前の方で止まってしまったら。この問題と同じ考え方をすれば、それが理想値に止まっているか、あるいは誤差１の確率がどのぐらいであるか、計算することができます。温度や集中力の残り具合によってはもう１度押し込むという選択肢が取れるので、僅かですが有利になることもあります。
戻りタイプ以外では、せいぜいたたき変化の半減ターンか集中力変化の会心ターンがないと使いにくいと思います。